Improve math skills of your kids - Learn step-by-step arithmetic from Math games

Math: Unknown - Step-by-step math calculation game for iOS.


Math: Unknown is much more than a math game. It is a step-by-step math calculation game which will teach users how to calculate in the correct order rather than just asking only the final calculated results.

The app consists of four basic arithmetic operations which are addition, subtraction, multiplication and division. In order to get started, users who are new to arithmetic can learn from animated calculation guides showing step-by-step procedures of solving each type of operation. It is also helpful for experienced users as a quick reference.

Generally, addition and subtraction may be difficult for users who just start learning math especially when questions require carrying or borrowing (also called regrouping). The app helps users to visualize the process of carrying and borrowing in the way it will be done on paper. Once users understand how these operations work, they are ready to learn multiplication and division.

For most students, division is considered as the most difficult arithmetic operation to solve. It is a common area of struggle since it requires prior knowledge of both multiplication and subtraction. To help users understand division, the app uses long division to teach all calculation procedures. Relevant multiplication table will be shown beside the question. Users will have to pick a number from the table which go into the dividend. Multiplication of selected number and divisor is automatically calculated, but the users have to do subtraction and drop down the next digit themselves. Learning whole calculation processes will make them master it in no time.

Math: Unknown is a helpful app for students who seriously want to improve arithmetic calculation skills.

Motion Simulation with Microsoft Excel



Motion Simulation with Microsoft Excel

Mechanical design usually deals with movement of several parts. There are a lot of softwares that help simulate the movement of concerned parts of machines such as UG, Solid Edge, Solid Work, etc.

But how do you make simulation without those softwares?

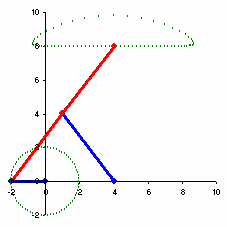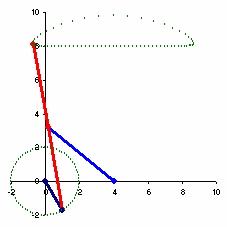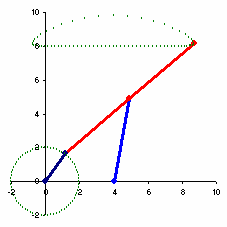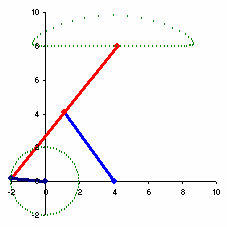
I use Microsoft Excel to do the simulation of my timing diagram. Watch the video.

Actually it is nothing but motion simulation using graphing method in Microsoft Excel. It cannot simulate all of your complex movements, but it helps you get the feeling of how your machine will behave according to your timing diagram.

This technique uses VBA (Visual Basic for Application) to control the movements. What you have to do is to prepare the excel spreadsheet with the table defining the sketch of your machine parts to be used in simulation. You have to set the formula in excel spreadsheet to manipulate the location (x,y) and rotation (angle). After proper settings, just let VBA code, which is embedded in Microsoft Excel, changes the control values in the manipulation table (the x-y chart is linked to this table). Then you can control the movement of parts that move in translation or rotation. For example, I use an indexing box at my transport conveyor which has 4 stops and the cam profile is MS (Modified Sine). So I put MS function into my VBA code and I can see how my conveyor is moving at the same as others.

Example of Modified Sine Movement Function.

=================================================================
' Modified Sine function
' T is dimensionless
' hm is stroke of movement

Function MS(T As Double, hm As Double)
Const PI = 3.14159265358979
Dim T5 As Double, T6 As Double
Dim V1 As Double, V2 As Double, V3 As Double, V4 As Double, V5 As Double, V6 As Double
Dim S1 As Double, S2 As Double, S3 As Double, S4 As Double, S5 As Double, S6 As Double
Dim Am As Double
Dim s As Double

Const T1 = 0.125
Const T2 = 0.125
Const T3 = 0.5
Const T4 = 0.5

T5 = 1 - T1
T6 = T5
Am = 1 / (2 * T1 / PI + (2 - 8 * T1) / PI ^ 2)

V1 = 2 / PI * T1 * Am
V2 = V1
V5 = V1
V6 = V1

V3 = 2 / PI * (T3 - T2) * Am + V2
V4 = V3

S1 = 2 * T1 ^ 2 / PI * Am - (2 * T1 / PI) ^ 2 * Am
S2 = S1

S3 = (2 / PI * (T3 - T2)) ^ 2 * Am + V2 * (T3 - T2) + S2
S4 = S3

S5 = 1 - S1
S6 = S5

Select Case T
Case 0 To T1
s = 2 * T1 / PI * Am * (T - 2 * T1 / PI * Sin(PI * T / (2 * T1)))
Case T2 To T3
s = (2 / PI * (T3 - T2)) ^ 2 * Am * (1 - Cos(PI * (T - T2) / (2 * (T3 - T2)))) + V2 * (T - T2) + S2
Case T4 To T5
s = 2 / PI * (T5 - T4) * Am * (2 / PI * (T5 - T4) * Sin(PI * (T - T4) / (2 * (T5 - T4))) - (T - T4)) + V4 * (T - T4) + S4
Case T6 To 1
s = (2 / PI * (1 - T6)) ^ 2 * Am * (Cos(PI * (T - T6) / (2 * (1 - T6))) - 1) + V6 * (T - T6) + S6
Case Else
s = 1
End Select

MS = s * hm

End Function
=================================================================

For those who are interested in downloading the example file, please click the link below


DOWNLOAD EXAMPLE FILE FOR FREE
Extract the zip file with password: mechanical-design-handbook.blogspot.com

Comments

Post a Comment

Popular posts from this blog

Dowel Pins and Locating Pins

Image
Dowel pins are the fasteners used to secure two parts together. They are available in both Metric and English sizes, and carry specifications such as diameter, length, and materials. Most dowel pins are made of stainless steel, plastic, , hardened steel, or ground steel. Plastic dowel pins are made of thermoplastic or thermosetting polymers with high molecular weight. Stainless dowel pins are chemical and corrosion resistant, and have relatively high pressure ratings. Dowel pins are often used as precise locating devices in machinery. Stainless dowel pins are machined to tight tolerances, as are the corresponding holes, which are typically reamed. A dowel pin may have a larger diameter so that it must be pressed into its hole or a smaller diameter than its hole so that it freely slips in. When mechanical design engineers design the mechanical components, typically they use dowel holes as reference points to control positioning variations and attain repeatable assembly quality. If...
Read more about this Mechanical Design Article »

Hoekens Straight-line Mechanism

Image
The Hoekens linkage is a four-bar mechanism that converts rotational motion to approximate straight-line motion. The Hoekens linkage is a cognate linkage of the Chebyshev linkage . " DESIGN OF MACHINERY " by Robert L. Norton shows the link ratios that give the smallest possible structural error in either position or velocity over values of Δβ from 20° to 180°. The followings are some interesting examples of Hoekens straight-line mechanism from youtube. Walking robot Marble machine Source: http://www.designofmachinery.com/DOM/Chap_03_3ed_p134.pdf http://en.wikipedia.org/wiki/Hoekens_linkage http://www.youtube.com/watch?v=AkI1nrq9mMQ http://www.youtube.com/watch?v=-CKgP_cueEw http://www.youtube.com/watch?v=PxpRUpmRdCY  
Read more about this Mechanical Design Article »

Ball Detent Torque Limiter: Overload Clutch

Image
A torque limiter is an automatic overload clutch that provides machine protection and reduces repair time during jamming load conditions. This is done to protect expensive machines and prevent physical injuries. A torque limiter may limit the torque by slipping (as in a friction plate slip-clutch), or uncouple the load entirely (as in a shear pin). Ideally the torque limiter should be placed as close as possible to the source of the jam. This will allow the system inertia and torque to be quickly and effectively disconnected from the jammed section. The system can then be allowed to stop without causing further machine damage. A mechanical torque limiter will provide faster response times and better protection than typical electronic methods at high crash rates. There are several disconnect types available, but we will focus at the Ball Detent type . A ball detent type torque limiter transmits force through hardened balls which rest in detents on the shaft and are held in pl...
Read more about this Mechanical Design Article »