Mechanical Design Handbook

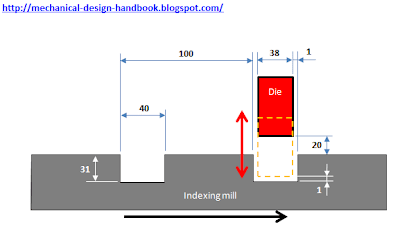
In post [ Timing Diagram (Part 1 - No Overlap Movement) ], we saw the design requirement that we have to design the die to work together with the indexing mill with the construction as shown below. Without detailed calculation, we could end up with a very simple timing diagram as shown below. But it's not good enough. The die has to wait for the indexing to finish its movement before moving. This reduces the indexing time of the die, and get high acceleration on the die. In post [ Timing Diagram (Part 2 - Maximum acceleration calculation) ], we calculated the maximum acceleration of Cycloidal motion cam profile and saw the opportunity to reduce the acceleration by extending the indexing time. In post [ Timing Diagram (Part 3 - Cycloid Cam Profile Analysis) ], we analyzed the cycloid cam profile and see opportunity of overlap motion. Some calculations have been made and we end up with new timing diagram which is smarter than the original one as shown below. We calculat

In previous post [ Timing Diagram (Part 2 - Maximum acceleration calculation) ], we calculated the maximum acceleration of the die using cycloid cam profile. We found out that this maximum acceleration of the die can be reduced if we can extend the indexing angle (B m ) or indexing time (t m ) through overlap motion. Then, let's see how we can calculate for the suitable indexing angle to reduce the acceleration of the die. Cycloidal motion cam profile has movement equation as follows. h = h m x [t/t m - 1/(2 x pi) x sin(2 x pi x t/t m )] Rearrange the equation to get h/h m = t/t m - 1/(2 x pi) x sin(2 x pi x t/t m ) The displacement profile can be plotted as shown below (dimensionless). We can see that at the first 10% of indexing time, the movement is just only 0.65% of the total movement (stroke) and at 90% of time, the remaining movement for the die is only 0.65% of the total movement (stroke). Or we can say that, there is not much movement at the first and last 1

Let's calculate the acceleration of the die from previous post [ Timing Diagram (Part 1 - No Overlap Movement) ] The die moves using Cycloid cam profile. So first we have to get the formula to calculate the maximum acceleration of cycloid cam profile. If the machine speed is N (pcs/h) and the indexing angle (degree) is B m , the indexing time (second) t m can be calculated as follows. Cycle time (sec) = 3600/N Indexing time t m (sec) = (B m /360) x Cycle time = (B m /360) x (3600/N) Hence, Indexing time t m (sec) = 10B m /N Cycloid cam profile has the equation of displacement as follows. h = h m x [t/t m - 1/(2 x pi) x sin(2 x pi x t/t m )] where: h m : Maximum displacement (m) t m : Indexing time (s) pi: 3.141592654 We can get velocity equation by differentiation. v = dh/dt = h m x [1/t m - (2 x pi)/(2 x pi x t m ) x cos(2 x pi x t/t m )] v = h m /t m x [1 - cos(2 x pi x t/t m )] Then, the acceleration is as follows. a = d 2 h/dt 2 = dv/dt = h m /t

When I search in Google for " timing diagram ", I found a lot of results about electrical timing diagram software but they're not about what I'm going to tell. Timing Diagram in my meaning is a tool that represents the sequences of movement of mechanisms. It is a very useful diagram for mechanical design engineers to understand how each part of the machine works together. " By properly design the timing diagram, we can make machine moves smoother even at higher speed. " We often draw the timing diagram using cam angle (in degree) in horizontal axis and use the movement of mechanism (in mm) in vertical axis. From the timing diagram, we can find the opportunity to reduce the acceleration (force) of the moving parts so as to reduce the wear in machine. Experience shows that a lot of mechanisms have been designed without using "overlap" movement. This makes the machine parts move from one point to another point in short period. But if we provide

In the previous post ( Standards of limits and fits for mating parts ), we talked about the definitions of each term related to limits and fits as well as the formulas to determine the values of tolerances. In this post, we're going to convert those information into the real calculation using Microsoft Excel (as usual). As stated earlier, the calculation results may be different from the real values used in general mechanical design handbook. So please use this just for educational purpose only, but use the real table from general limits and fits table if you want to get higher accuracy values. This is the screen shot of excel file to calculate upper deviation and lower deviation according to the selected shaft diameter and tolerance grade. Let's see how to manually calculate the deviation values before using the program. Example: To calculate the upper deviation and lower deviation of a shaft with diameter of 40 mm and tolerance g6. Please refer to previous post (

METRIC STANDARDS FOR LIMITS & FITS Definitions 1. Basic size is the size to which limits or deviations are assigned and is the same for both members of a fit. It is measured in millimeters. 2. Deviation is the algebraic difference between a size and the corresponding basic size. 3. Upper deviation is the algebraic difference between the maximum limit and the corresponding basic size. 4. Lower deviation is the algebraic difference between the minimum limit and the corresponding basic size. 5. Fundamental deviation is either the upper or the lower deviation, depending on which is closest to the basic size. 6. Tolerance is the difference between the maximum and minimum size limits of a part. 7. International tolerance grade (IT) is a group of tolerances which have the same relative level of accuracy but which vary depending on the basic size. 8. Hole basis represents a system of fits corresponding to a basic hole size. 9. Shaft basis represents a system of fits cor

Major types of flexible mechanical power transmission are belts and chains. Belts operate on pulleys or sheaves, whereas chains operate on toothed wheels called sprockets. When to use chain drives or belt drives ? Electric motors typically operate at too high speed e.g. 1500 rpm and deliver too low torque e.g. 1.8 N.m to be appropriate for the final drive application. These figures are taken from 0.25 kW motor specs of some manufacturers just to get an idea. For a given power transmission, the torque is increased in proportion to the amount that rotational speed is reduced. So the method of speed reduction is usually required for normal mechanical power transmission system. Usually, we use belt drives for first stage reduction because of high speed of the motor. A smaller drive pulley is attached to the motor shaft which runs at high speed, while a larger diameter pulley is attached to the parallel shaft that operates at a correspondingly lower speed. " Usually, we use belt driv

Every design approach, we must ensure that the stress level is below the yield in ductile materials , automatically ensuring that the part will not break under a static load. For brittle materials , we must ensure that the stress levels are well below the ultimate tensile strength . Two other failure modes that apply to machine members are fatigue and wear. Fatigue is the response of a part subjected to repeated loads. Wear often happens where two parts are in contact with each other such as gears, bearings, and chains, for which it is a major concern. source: Machine Elements in Mechanical Design, Robert L. Mott

Chain Sprockets are fabricated from a variety of materials; this would depend upon the application of the drive. Large fabricated steel chain sprockets are manufactured with holes to reduce the weight of the chain sprocket on the equipment. Because roller chain drives sometimes have restricted spaces for their installation or mounting, the hubs are made in several different styles. Type A chain sprockets are flat and have no hub at all . They are usually mounted on flanges or hubs of the device that they are driving. This is accomplished through a series of holes that are either plain or tapered. Type B chain sprockets has a hub on one side and extend slightly on the other side. The hub is extended to one side to allow the sprocket to be fitted close to the machinery that it is being mounted on. This eliminates a large overhung load on the bearings of the equipment. Type C chain sprockets are extended on both sides of the plate surface. They are usually used on the driven sprocket

Chain drives are an important part of a conveyor system. Chain drive s are normally used to transmit power between a drive unit and a driven unit of the conveyor system. Chain drives can consist of one or multiple strand chains, depending on the load that the unit must transmit. The chains need to be the matched with the sprocket type, and they must be tight enough to prevent slippage. " Chain is sized by the pitch or the center-to-center distance between the pins. This is done in 1/8" increments. " Conveyor Roller Chain Roller chains are made up of roller chain link that are joined with pin links. The roller chain links are made up of two side bars, two rollers, and two bushings. The roller reduces the friction between the chain and the sprocket, thereby increasing the life of the unit. Roller chains can operate at faster speeds than plain chains , and properly maintained, they will offer years of reliable service. Some roller chains come with a double pitch ,

Dowel pins are the fasteners used to secure two parts together. They are available in both Metric and English sizes, and carry specifications such as diameter, length, and materials. Most dowel pins are made of stainless steel, plastic, , hardened steel, or ground steel. Plastic dowel pins are made of thermoplastic or thermosetting polymers with high molecular weight. Stainless dowel pins are chemical and corrosion resistant, and have relatively high pressure ratings. Dowel pins are often used as precise locating devices in machinery. Stainless dowel pins are machined to tight tolerances, as are the corresponding holes, which are typically reamed. A dowel pin may have a larger diameter so that it must be pressed into its hole or a smaller diameter than its hole so that it freely slips in. When mechanical design engineers design the mechanical components, typically they use dowel holes as reference points to control positioning variations and attain repeatable assembly quality. If

A linear induction motor is made up of an inductor which is made of individual cores with a concentrated poly phase. Linear induction motor can be directly substituted for ball screw drives, hydraulic drives, pneumatic drives, or cam drives . A linear induction motor is basically what is referred to by experts as a “rotating squirrel cage” induction motor . The difference is that the motor is opened out flat. Instead of producing rotary torque from a cylindrical machine it produces linear force from a flat machine. The shape and the way it produces motion is changed, however it is still the same as its cylindrical counterpart. There are no moving parts, however and most experts don’t like that. It does have a silent operation and reduced maintenance as well as a compact size, which appeals many engineers. There is also a universal agreement that it has an ease of control and installation. These are all important considerations when thinking about what type of device you want to crea

Mechanical energy is an area of science that is making strides every day. The study of how actuators produce mechanical motion by converting various forms of energy into mechanical energy is a source of great exploration. Science finds new ways to make use of actuators every day including for medical purposes. Many scientists believe that the more they study these seemingly simple machines, the more they will discover ways of helping mankind. The way in which a linear actuator works is that there is a motor that rotates a drive screw using a synchronous timing belt drive. Some linear actuators can also use a worm gear drive or direct drive. Whichever the choice, the turning of the screw pushes a drive nut along the screw, which in turn pushes the rod out and the rotating the screw in the opposite direction will retract the rod. According to the Association of Sciences, the drive screw is either an ACME or ball thread or is belt-driven which is what gives the machine its motion. A cov

Modern automotive brake was invented in the late 19th century, around the same time as the tyre. Up until then, vehicles had wooden wheels that were stopped by large wooden blocks, lowered into position by the driver using a simple lever system. When tyres were invented, the wooden block system was not good enough to stop them at the higher speeds they could achieve, which meant that a new braking system had to be invented. To see the basic principles of modern automotive braking , it is easiest to look at a bicycle. Basically, when you put pressure on the brakes, the pressure is transferred through cables to pull small brake pads onto the side of the tyres, and the force of the friction against the tyres causes them to stop. In fact, cars originally used this very same cable system, but it was found not to work so well at high speeds. Instead, the cables were replaced with hydraulic fluid , which works to transfer the pressure the driver puts on the pedal to the brakes. This works b

Whether you drive a Chevrolet, a cycle, a van or a pickup truck, you probably have disc brake pads on your vehicle. And even though you probably never think about their function, they are the single most important function on your vehicle. Though there are several types of motor brakes , disc brakes , drum brake , caliper brakes , etc. but the disk brakes are more commonly used. Disc brakes are far better than drum brakes because of their powerful stopping ability. Disc brake pads handle substantially better in wet weather conditions. Why choose anything but the best? What are Disc Brakes ? Put simply, disc brakes consist of two disc brake pads that grasp a rotating disk . The disk, or rotor, connects to the wheels by an axle. You control the grasping power. When you pull on the brake, the clamps come together on the disk, forcing it to stop spinning and causing your vehicle to slow down and eventually stop. How Do You Control Disk Brakes ? In a car, controlling your disk brake

Many bearings look very similar, whether they are ball bearings, roller bearings or other bearings. What?! Other bearings? What is a ball bearing, anyway? Ball bearings are formed with an outer ring, an inner ring, a cage or a retainer inside, and a rolling element inside, typically a ball (which is why they are called ball bearings). Roller bearings are formed using a roller instead of a ball, which is why they are called roller bearings (Yes, finally something that makes sense!). Other bearings look just like metal tubes, called plain bearings or bush bearings. They look like sawed off pipe or tube. The principle of bearings is the same principle behind the wheel: things move better by rolling than by sliding. They are called "bearings" because they bear the weight of the object, such as an inline skate or the head of dentist's drill, allowing the object to glide over them with incredible ease and speed. Unlike wheels, they don't turn on an axel; they turn on

Robots as we all know are considered as friendly creature created by human beings as we are created by God. They are created for human being to simplify life even more basically for our daily chores with the specified sequence and even by military for the purpose of doing things which has the danger to life of human beings and thus they are developed over years to substitute human beings in all the fields. Many of us are not that qualified to make a robot by ourselves and that why we all are anxious to know how to make a robot and even depends upon the task we want to create it for. We all have the tendencies of exploring whatever new comes in the field of science and hence a basic prototype robot can be created knowing few basic high end programming stuffs. Robots are almost 30% programming and hence if we target one specific purpose and program it well enough then it serves our purpose and the program mostly used for this is Unix and for beginner's Lego Mindstorms series is th

Sir Isaac Newton first presented his three laws of motion in the " Principia Mathematica Philosophiae Naturalis " in 1686. Let's start with the First law of Newton , which states: In the absence of external influences, a material body remains in a condition of rest or continues in uniform and rectilinear movement through inertia . This law is also known as " the law of inertia ". And what is inertia? As a matter of fact, it describes the ability of a body to preserve the initial parameters of its own motion. The formula of the Newton's second law is: F = m • a , where F = the size of the external force, m = size of inert mass, a = size of the acceleration of a body. If we rewrite this as: a = F / m it becomes obvious, that the larger the mass of a body, the greater external effort is required to apply the same acceleration to it. Actually, inertial mass here acts as a measure of its own internal resistance to the influence of the external force. The third

The following four-article series was published in a newsletter of the American Society of Mechanical Engineers (ASME) . It serves as an introduction to the recent analysis discipline known as the finite element (FEM). The author is an engineering consultant and expert witness specializing in finite element analysis. FINITE ELEMENT ANALYSIS: Post-processing by Steve Roensch, President, Roensch & Associates Last in a four-part series After a finite element model has been prepared and checked, boundary conditions have been applied, and the model has been solved, it is time to investigate the results of the analysis. This activity is known as the post-processing phase of the finite element method. Post-processing begins with a thorough check for problems that may have occurred during solution. Most solvers provide a log file, which should be searched for warnings or errors, and which will also provide a quantitative measure of how well-behaved the numerical procedures were

The following four-article series was published in a newsletter of the American Society of Mechanical Engineers (ASME) . It serves as an introduction to the recent analysis discipline known as the finite element method (FEM). The author is an engineering consultant and expert witness specializing in finite element analysis. FINITE ELEMENT ANALYSIS: Solution by Steve Roensch, President, Roensch & Associates Third in a four-part series While the pre-processing and post-processing phases of the finite element method are interactive and time-consuming for the analyst, the solution is often a batch process, and is demanding of computer resource. The governing equations are assembled into matrix form and are solved numerically. The assembly process depends not only on the type of analysis (e.g. static or dynamic), but also on the model's element types and properties, material properties and boundary conditions. In the case of a linear static structural analysis, the assembled equa

The following four-article series was published in a newsletter of the American Society of Mechanical Engineers (ASME) . It serves as an introduction to the recent analysis discipline known as the finite element method (FEM). The author is an engineering consultant and expert witness specializing in finite element analysis. FINITE ELEMENT ANALYSIS: Pre-processing by Steve Roensch, President, Roensch & Associates Second in a four-part series As discussed in Finite Element Analysis (FEA): Introduction , finite element analysis is comprised of pre-processing, solution and post-processing phases. The goals of pre-processing are to develop an appropriate finite element mesh, assign suitable material properties, and apply boundary conditions in the form of restraints and loads. The finite element mesh subdivides the geometry into elements , upon which are found nodes . The nodes, which are really just point locations in space, are generally located at the element corners and perhaps nea

The following four-article series was published in a newsletter of the American Society of Mechanical Engineers (ASME) . It serves as an introduction to the recent analysis discipline known as the finite element method (FEM). The author is an engineering consultant and expert witness specializing in finite element analysis. FINITE ELEMENT ANALYSIS: Introduction by Steve Roensch, President, Roensch & Associates First in a four-part series Finite element analysis (FEA) is a fairly recent discipline crossing the boundaries of mathematics, physics, engineering and computer science. The method has wide application and enjoys extensive utilization in the structural, thermal and fluid analysis areas. The finite element method is comprised of three major phases: (1) pre-processing , in which the analyst develops a finite element mesh to divide the subject geometry into subdomains for mathematical analysis, and applies material properties and boundary conditions. (2) solution , during whic

When designing the machine for the customers in Europe, I have to make sure that the machine has full CE compliance. By the way, what is CE? I search for more details about CE and put them here for more understanding. The CE marking is an acronym for the French " Conformité Européenne ". By affixing the CE marking , the manufacturer, or in certain cases another legal person responsible for the product, asserts that the item meets all the essential "Health and Safety" requirements of the relevant European Directive(s) that provide for the CE marking . Examples of European Directives requiring CE marking include toy safety, machinery, low-voltage equipment, medical devices and electromagnetic compatibility. CE Marking Procedure The "New Approach" to conformity enables manufacturers to use what is called as "SELF DECLARATION" where the manufacturer himself declares conformity by signing the "Declaration of Conformity (DOC)" and then affi