Polynomial Cam Function (Fifth-degree polynomial Example) - Part 4

In the post [Polynomial Cam Function (Fifth-degree polynomial characteristics) - Part 3], we know the characteristics of Fifth-degree polynomial cam profile. In this post we will see the example of using Fifth-degree polynomial together with Linear cam functions to improve the movement of mechanism. We can use the same example as what we did in the post [Timing Diagram (Part 4 - Timing Diagrams Comparison using Motion Simulation in Microsoft Excel)]. The original maximum acceleration of the die for that case without any overlap motion was 4.154 m/s². But we did the improvement using cycloid cam curve and the maximum acceleration reduced to 0.804 m/s². That was a big improvement on the acceleration of the mechanism. This time we can find that using Fifth-degree (3-4-5) polynomial cam function can also considerably reduce the maximum acceleration of the mechanism in the same level as cycloid cam profile. But the comparison between cycloid and fifth-degree polynomial for this case is not that significant. This is just to show how to use it. And please note that it doesn't mean that lowest acceleration is best movement for this kind of application. This is just only the example of using overlapping motion with fifth-degree polynomial cam profile.

Our constraints for this motion is still the same as previous example, the total displacement is 50 mm and the die has to move inside the hole for 30 mm. The die has to be away from the indexing mill surface about 1 mm before indexing mill really moves.

Please note that the velocity and acceleration functions derived in previous post has the unit of mm/rad and mm/rad² respectively. To change the angular domain to time domain, we have to multiply velocity function and acceleration function by omega and omega² respectively. Where omega is the angular velocity of cam shaft in rad/s. This is when v₀ and v₁ are in mm/rad and b_m in deg. But normally it's easier to use v₀ and v₁ in mm/deg and b_m in deg. So the unit of omega should be deg/s.

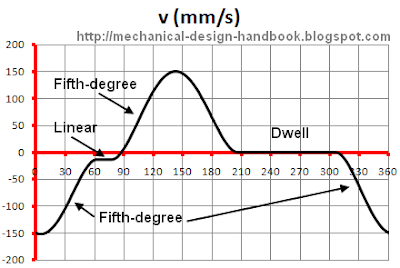
We can work out in more details and get the following displacement, velocity and acceleration profiles as shown in the following graphs.

Sector   Function        Start Angle   End Angle    h1         h2
   A-B     Linear             62                77                1.43       0.43
   B-C     Fifth-degree     77                206              0.43        50
   C-D     Dwell             206               306                50         50
   D-A     Fifth-degree    306                62                 50        1.43

We know that fifth-degree (3-4-5) polynomial cam function needs 2 extra parameters i.e. v₀ and v₁ to define the full curve of each sector. For this example, the linear cam function is used between 2 fifth-degree polynomial sectors. The slope of linear cam function then defines values of v₁ and v₀ of first and second fifth-degree polynomial cam curves respectively.

The slope of linear cam function can be calculated from (0.43-1.43)/(77 -62) = -0.0667. And this value is the value of v₁ of sector D-A and is the value of v₀ of sector B-C. This is to make sure that there is no discontinuity at the connecting point between velocity cam profiles.

Remark about displacement profile: The fifth-degree polynomial displacement function derived previously has zero displacement as starting point and end with total lift of h_m. To connect it with other curve, we must add another value called h_start in order to avoid discontinuity in displacement cam curve. Find more details in the Excel spreadsheet example file.

A simple excel spreadsheet is developed as shown below to calculate for displacement, velocity and acceleration over the entire cycle of movement. Graphing function in Microsoft Excel makes it easy to visualize any discontinuity that may have. We can also simply trace all the displacement, velocity and acceleration over all sectors. With excel graph, we can easily find the sector that creates highest acceleration (absolute value of both positive and negative acceleration) and can modify the timing diagram until we get the best result.

In the excel spreadsheet, you can see motion simulation to compare between movement using cycloid and fifth-degree polynomial.

 
FREE DOWNLOAD EXCEL FILE OF TIMING DIAGRAM OVERLAP MOTION WITH FIFTH-DEGREE POLYNOMIAL CAM FUNCTION.

Extract the zip file with password: mechanical-design-handbook.blogspot.com